The Importance of Picking the Right Job Title for Your Job
Job titles are often the first interaction between job seekers and employers. As a job seeker searches, they click relevant titles before getting to know the role more deeply through its job description. Calling a job “software engineer” versus “programmer” will likely lead to a different number of applicants and proportion of those meeting the minimum qualifications, but just how different? Surprisingly, after a single word change in nearly identical job titles, we observed more qualified candidates and more total candidates. This post describes our initial research and how we can improve on this in the future.
Data and Product Science at Indeed
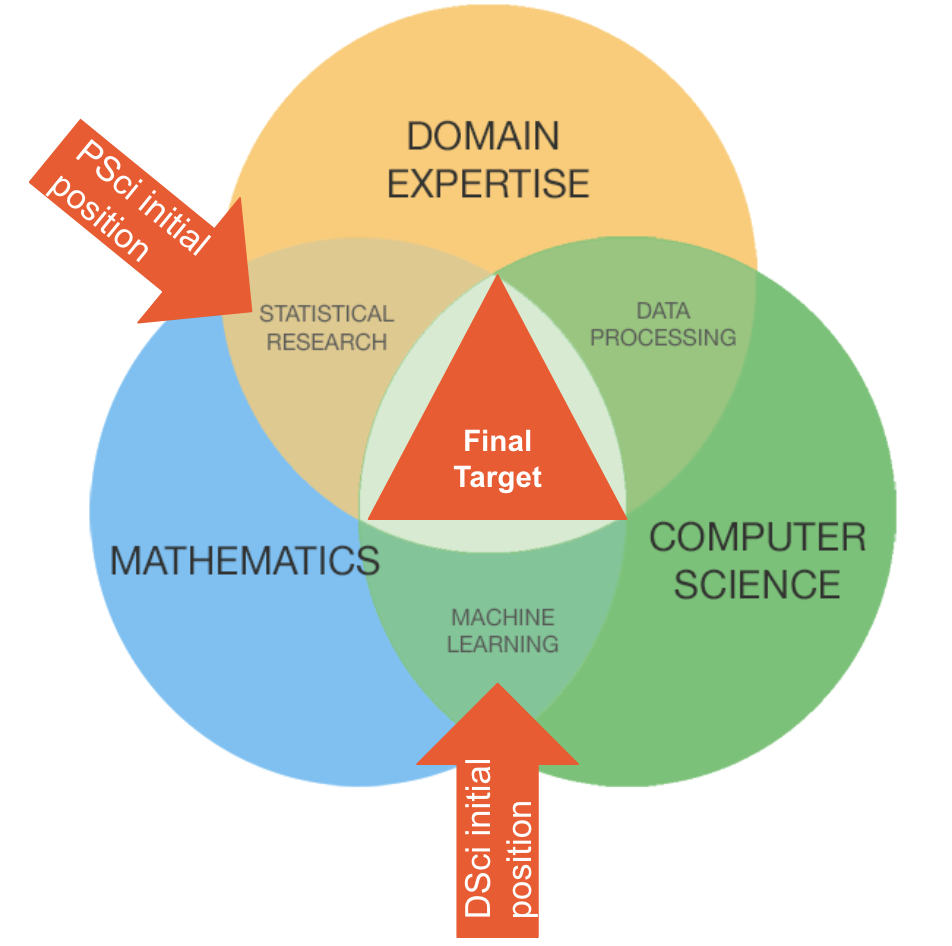
There are two main roles in Indeed’s Data Science organization — data scientists and product scientists. Indeed currently has data/product scientists in five offices: Austin, San Francisco, Seattle, Singapore, and Tokyo, working on a wide variety of product and engineering teams.
Both roles employ advanced statistical and machine learning techniques to help people get jobs. Data science has a higher emphasis on machine learning and software engineering, while product science focuses on experiments, analysis, and simpler models that can improve the product. In short, data scientists are closer to software engineering than product management, and vice versa for product scientists.
You can view the differences in the job descriptions here: (Product Scientist/Data Scientist). Despite their differences, the ultimate requirements for data and product scientists are essentially the same: a deep understanding and experience in mathematics and computer science, and domain expertise.
Sequential test: Changing the job title
To find out how job titles affect the hiring process, we conducted an experiment and changed the Product Scientist title to “Data Scientist: Product” in Seattle and “Product Scientist: Data Science” in San Francisco on March 15, while keeping the job title unchanged for Austin. Job descriptions remained the same for all three cities.
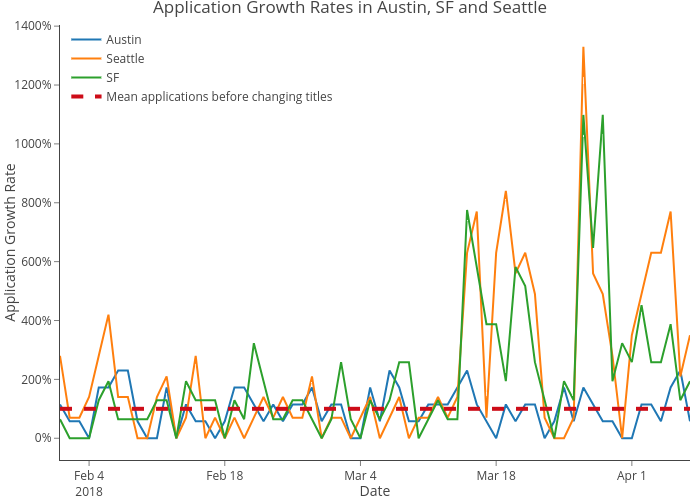
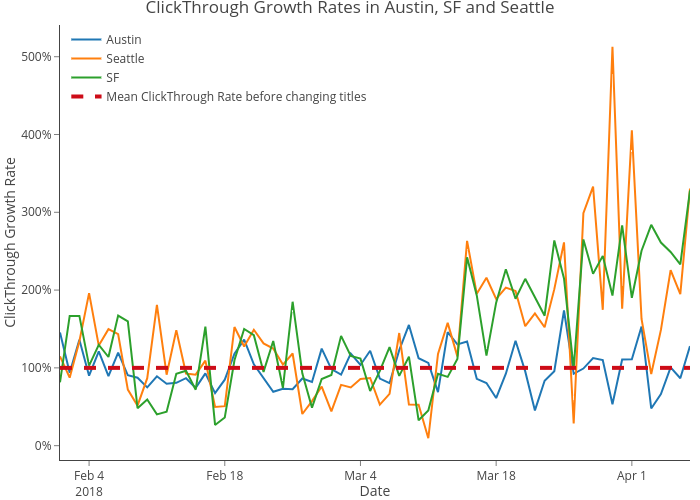
Engineering work was required for an A/B test, so we chose to look at this sequentially. We conducted a statistical power analysis to determine the sample size ahead of time. We first compared the click-through rate (defined as clicks/impressions) and number of applies for the three cities before and after March 15. From the following two charts, we see both the number of applies and the click-through rate jumped up since March 15 for Seattle and San Francisco (SF). We performed t-tests that show that applies and clickthrough rates are significantly higher for Seattle and San Francisco than for Austin starting from March 15.
Click-through Growth Rates in Austin, San Francisco, and Seattle
However, changing the job titles might affect the job search ranking, and we know the top and bottom ranked jobs on a page usually have a higher probability of being clicked. In order to account for this position bias, we conducted a logistic regression to predict clicks on page, position on the SERP, city (Austin, Seattle or San Francisco), and whether we changed the job title. We also included the interaction term between city, and if we changed the job title to test the hypothesis that log-odds ratios for various cities are different after changing titles than before changing titles.
The regression equation was estimated¹ as follows:

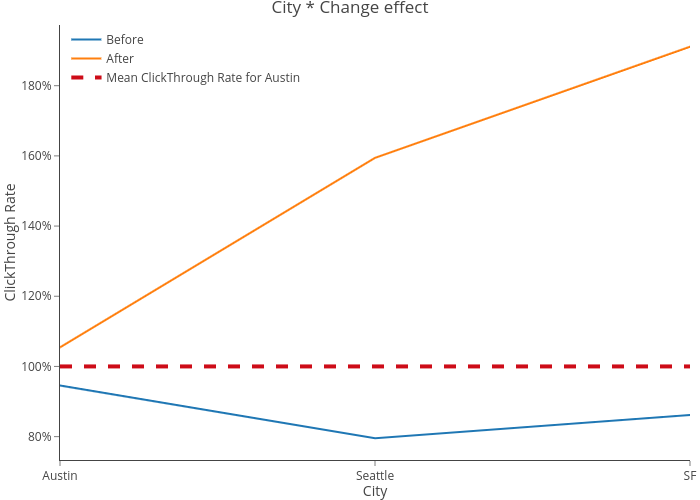
The non-parallel lines in the interaction plot below suggest that there are significant interaction effects, which the associated significant p-values for interaction terms confirms.
Before changing titles, the equation is simply:

Switching from Austin to Seattle yields a change in log odds of -0.18 and to San Francisco yields a change in log odds of -0.09.
After changing titles, the equation is:

Switching from Austin to Seattle yields a change in log odds of -0.18+0.6 = 0.42 and to San Francisco yields a change in log odds of -0.09+0.71 = 0.62
The graph below also confirms that log-odds ratio for Seattle and San Francisco are much higher after changing titles vs before changing titles. To sum up, we see significantly higher applicants for cities with changed titles.
Qualified application model
We see more applicants after changing titles, but is this pool of applicants more suitable for the role? A team at Indeed has developed a model that scores the likelihood of a resume containing skills and experiences that meet the requirements in a job description.
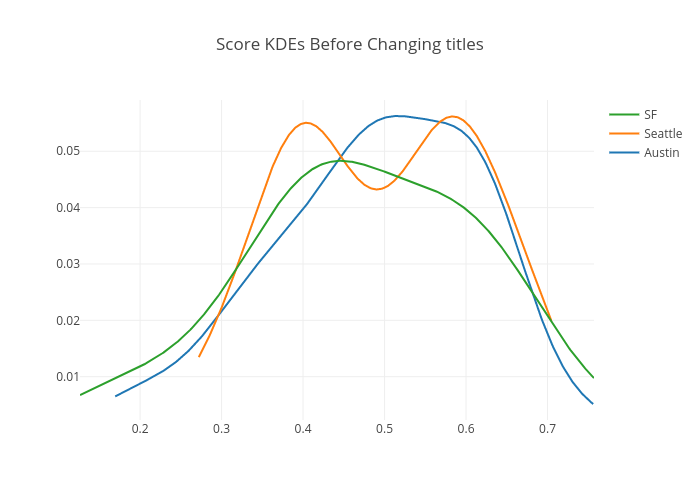
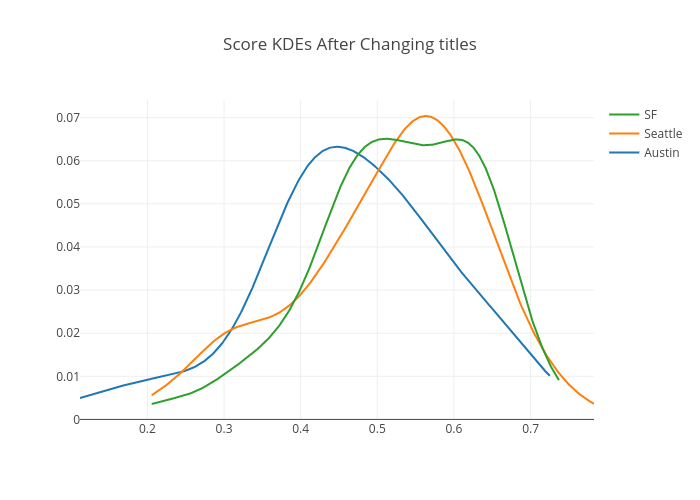
We applied this model to all candidates who applied for “Product Scientist” (before changing titles) from February 1 to March 14 and got the scores² for each candidate. The mean scores for Austin, Seattle and San Francisco were 0.489, 0.498, and 0.471 respectively. The plot below shows the score Kernel Density Estimation (KDE) for Austin, Seattle, and San Francisco, and the chart shows the p-values (insignificant) for t-tests and Kolmogorov-Smirnov (KS) tests. The KS test tries to determine if two samples are drawn from the same distribution. The test is nonparametric and makes no assumption about the data distribution. Both tests indicate that our applicant qualification rate was at the same level for all three locations before changing titles.
When the model was applied to all applicants after changing titles, the mean scores for Austin, Seattle, and San Francisco were 0.466, 0.516, 0.528 respectively. We observed a small decrease in the mean rate for Austin, accompanied by increases in Seattle and San Francisco. The plot below shows the score distributions for Austin, Seattle, and San Francisco. After controlling the False Discovery Rate to adjust for p-values, both tests indicate that applicant qualification rates with changed titles (Seattle and San Francisco) are significantly higher than those with the original title (Austin), while there is no significant difference between different changed titles (Data Scientist: Product and Product Scientist: Data Science).
Are you surprised by these findings? Our pilot research shows that simply making small changes to job titles led to more and better qualified candidates for Indeed. Job titles do matter, more than you think — they are great attention catchers and a prime focus as much as the job descriptions. So, you should care about your job titles and pick ones that can be noticed and easily stand out for job seekers.
For further reading, more rigorous approaches to establishing causal effect include:
- Randomized experimental design that you can deliberately change one or more factors in order to observe the effect of factors on one or more response variables.
- Causal inference models such as structural equation modeling³ and Rubin causal model⁴ can be used to analyze causal effect statistically in both observational and experimental studies.
If you are interested in using the scientific method to improve or develop products and help people get jobs, check out our open Product Scientist and Data Scientist positions at Indeed!
This is the second article in our ongoing series about Data Science from Indeed. The first article is There’s No Such Thing as a Data Scientist from our colleague, Clint Chegin.
Footnotes:
1. P-value for the hypothesis test for which the Z value is the test statistic. It tells you the probability of a test statistic being at least as unusual as the one you obtained, if the null hypothesis were true (the coefficient is zero). If this probability is low, it suggests that it would be rare to get a result as unusual as this if the coefficient were really zero. Signif. code is associated to each estimate and is only intended to flag levels of significance. The more asterisks, the more significant p-values are. For example, three asterisks represent a highly significant p-value (if p-value is less than 0.001).
2. These model scores are non-standardized and not probabilities. An application score of 0.8 represents a higher likelihood relative to an application with a score of 0.4 (but doesn’t mean twice as likely).
3. Bollen, K.A.; Pearl, J. (2013). “Eight Myths about Causality and Structural Equation Models”. In Morgan, S.L. Handbook of Causal Analysis for Social Research. Dordrecht: Springer. pp. 301–328.
4. Sekhon, Jasjeet (2007). “The Neyman–Rubin Model of Causal Inference and Estimation via Matching Methods” (PDF). The Oxford Handbook of Political Methodology.
Cross-posted on Medium.